发表于 | Edited on | 分类于
Symbols count in article： 76 | Reading time ≈ 1 mins.

1. 怎样由源数据构造高斯分布数据。

中心极限定理是说，对任意分布的随机变量，取n个样本，当n很大时，n个样本的平均值服从高斯分布，均值为原分布均值

发表于 | Edited on | 分类于
Symbols count in article： 1.9k | Reading time ≈ 4 mins.

###

导读:FAIR(Facebook AI Reaearch) 何恺明团队最新论文提出 “全景 FPN”，聚焦于图像的全景分割任务，将分别用于语义分割和实例分割的FCN和Mask R-CNN结合起来，设计了 Panoptic FPN。该方法可能成为全景分割研究的强大基线。

全景特征金字塔网络 Panoptic FPN

Panoptic FPN 是一个简单的、单网络的 baseline，它的目标是在实例分割和语义分割以及它们的联合任务：全景分割上实现最高性能。
设计原则是：从具有FPN Mask R-CNN 开始，进行最小的修改，生成一个语义分割的 dense-pixel 输出。
模型架构如下：

####特征金字塔网络 (Feature Pyramid Network)：

首先简要回顾一下 FPN。FPN 采用一个具有多空间分辨率特征的标准网络 (如 ResNet)，并添加一个具有横向连接的自上而下的通道，如图 1a 所示。自上而下的路径从网络的最深层开始，并逐步向上采样，同时添加自底向上路径的高分辨率特性的转换版本。FPN 生成一个金字塔，通常具有 1/32 到 1/4 的分辨率，其中每个金字塔级别具有相同的通道维度 (默认是 256)。

####实例分割分支：

FPN 的设计，特别是对所有金字塔级别使用相同的通道维数，使得附加基于区域的对象检测器变得很容易，比如 Faster R-CNN。 为了输出实例分段，我们使用 Mask R-CNN，它通过添加 FCN 分支来预测每个候选区域的二进制分段 Mask，从而扩展 Faster R-CNN.

Panoptic FPN：

如前所述，我们的方法是使用 FPN 对 Mask R-CNN 进行修改，实现像素级语义分割预测。然而，为了实现准确的预测，该任务所使用的特性应该具备以下特征：

  • 1 具有适当的高分辨率，以捕获精细的结构;
  • 2 编码足够丰富的语义，以准确地预测类标签;
  • 3 虽然 FPN 是为目标检测而设计的，但是这些要求——高分辨率、丰富的、多尺度的特征——正好是 FPN 的特征。因此，我们建议在 FPN 上附加一个简单而快速的语义分割分支。

实验和结果

我们的目标是证明我们的方法，Panoptic FPN，可以作为一个简单有效的单网络 baseline，用于实例分割、语义分割，以及他们的联合任务全景分割。
因此，我们从测试语义分割方法 (我们将这个单任务变体称为 Semantic FPN) 开始分析。令人惊讶的是，这个简单的模型在 COCO 和 Cityscapes 数据集上实现了具有竞争力的语义分割结果。
接下来，我们分析了语义分割分支与 Mask R-CNN 的集成，以及联合训练的效果。最后，我们再次在 COCO 和 Cityscapes 数据集上展示了全景分割的结果。定性结果如表 2 和表 6 所示。

###多任务训练

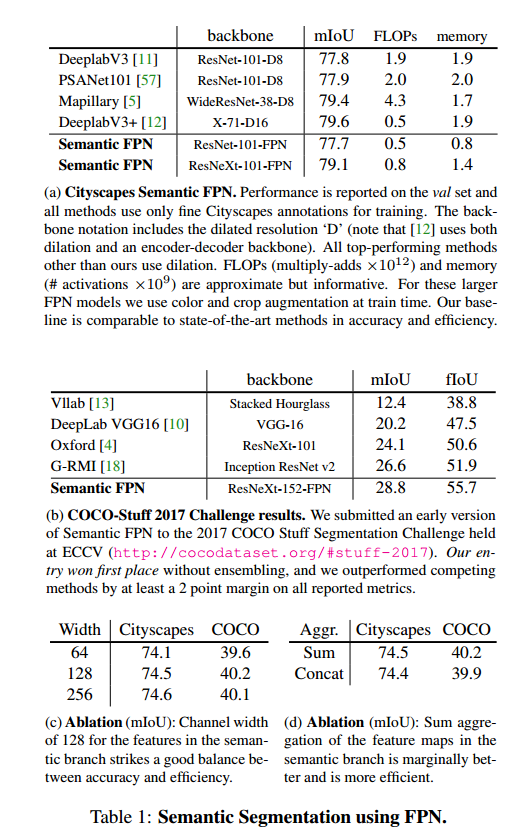
我们的方法在单任务上表现非常好；对于语义分割，上一节的结果证明了这一点；对于实例分割，这是已知的，因为该方法基于 Mask R-CNN。但是，我们是否可以在多任务环境中共同训练这两项任务呢?
为了将我们的语义分割分支与 Mask R-CNN 中的实例分割分支结合起来，我们需要确定如何训练一个单一的、统一的网络。以往的研究表明，多任务训练往往具有挑战性，并可能导致结果精度下降。我们同样观察到，对于语义或实例分割，添加辅助任务与单任务基线相比会降低准确性。

表中，ResNet-50-FPN 的结果表明，使用一个简单的语义分割损失λs，或实例分割损失λi，结果可以改善单任务 baseline 的结果。具体来说，适当地添加一个语义分割分支λs 能改进实例分割，反之亦然。这可以用来改进单任务结果。然而，我们的主要目标是同时解决这两个任务，这将在下一节讨论。

###Panoptic FPN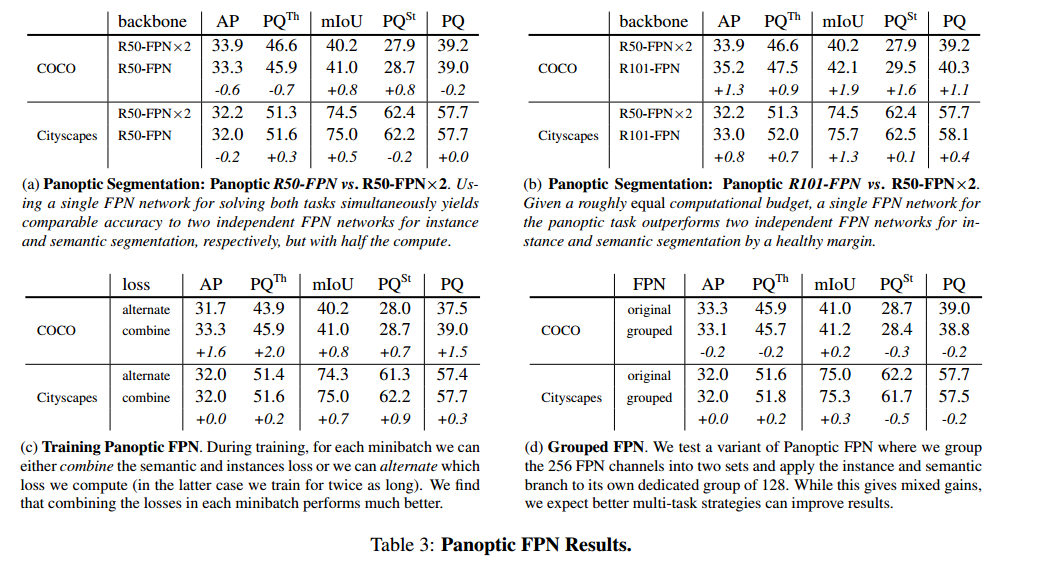

测试 Panoptic FPN 对于全景分割的联合任务的结果，其中网络必须联合并准确的输出 stuff 和 thing 分割。
主要结果：在表 3a 中，我们比较了使用相同骨架的 Panoptic FPN 分别训练的两个网络。Panoptic FPN 具有相当的性能，但只需要一半的计算量。
我们还通过比较两个单独的网络，分别是 Panoptic R101-FPN 和 R50-FPN×2，来平衡计算预算，见表 3b。使用大致相等的计算预算，Panoptic FPN 明显优于两个独立的网络。
综上所述，这些结果表明联合方法是有益的，我们提出的 Panoptic FPN 方法可以作为联合任务的可靠 baseline。

发表于 | 分类于
Symbols count in article： 708 | Reading time ≈ 1 mins.

1. [Windows] failed to create cublas handle: CUBLAS_STATUS_ALLOC_FAILED

以下可以解决问题 但是会有内存不足的W

{.line-numbers}
1
2
3
config = tf.ConfigProto()
config.gpu_options.allow_growth = True #创建session的时候允许显存增长
session = tf.Session(config=config)

Allocator (GPU_0_bfc) ran out of memory trying to allocate 1019.25MiB. The caller indicates that this is not a failure, but may mean that there could be performance gains if more memory were available.

如果你是使用 GPU 版 TensorFlow 的话，并且你想在显卡高占用率的情况下（比如玩游戏）训练模型，那你要注意在初始化 Session 的时候为其分配固定数量的显存，否则可能会在开始训练的时候直接报错退出：

{.line-numbers}
1
2
gpu_options = tf.GPUOptions(per_process_gpu_memory_fraction=0.333)  
sess = tf.Session(config=tf.ConfigProto(gpu_options=gpu_options))

发表于 | 分类于
Symbols count in article： 3.2k | Reading time ≈ 6 mins.

1. NMS算法(非极大值抑制算法)

该算法主要目的是筛选出重复框，保留有效框。
主要用在 region proposal阶段以及最后框出的阶段。
假设进行非极大值抑制的输入为2000x20的矩阵，2000表示该图像上框的个数，20表示类别数：
具体步骤如下：

  • 1 对2000×20维矩阵中每列按从大到小进行排序（每列表示一类，共20类。同一类可能有多个目标，如上图有两个人）；

  • 2 从每列最大的得分建议框开始，分别与该列后面的得分建议框进行IoU计算，若IoU>阈值，则剔除得分较小的建议框，否则认为图像中同一类物体有多个目标；两个同类的目标的建议框基本不会有重叠(因为两个同类在一张图片中肯定不会有大面积重叠啊)，因此去掉建议框重叠较大的实际上是实现了剔除同一个目标的重叠框

  • 3 从每列次大的得分建议框开始，重复步骤2；

  • 4 重复步骤3直到遍历完该列所有建议框；

  • 5 遍历完2000×20维矩阵所有列，即所有物体种类都做一遍非极大值抑制；

2. Batch Normalization reference

  • 为什么要进行特征归一化:
    • 归一化后加快了梯度下降求最优解的速度;
    • 归一化有可能提高精度;
  • 简单缩放 min-max
  • 标准差标准化 z-score 0均值标准化(zero-mean normalization)
    • 经过处理的数据符合标准正态分布，即均值为0，标准差为1，其转化函数为
  • 非线性归一化 比如log
  • add in 2019-03-18
  • 提出背景
    • 网络更新参数后使得输出的分布发生变化(即下一层的输入的分布发生变化)。网络参数需要不断调整来适应这种变化 因此会影响网络的学习速率。其次 还会使网络输出进入饱和区，减缓网络的收敛速度。此成为Internal Convarite shift。
    • 为解决这个问题 提出了归一化。即对每一个特征进行归一化，使其分布0均值 方差为1。
    • 具体解决方案：
      • BN。批归一化。即在每一个Batch的同一维度特征进行BN.
      • LN。层归一化。避开Batch维度 在每一个输入上进行归一化 H*W*C上的归一化。
      • IN。实例归一化。具体到某一次输入的每个channel上分别归一化。
      • GN。介于LN 和 IN 的之间 将channel进行分组 然后进行归一化操作。
        示意图

3.动量更新方法

  • 传统SGD更新方法。更新速度慢

    {.line-numbers}
    1
    x += -learning_rate * dx

  • momentum update

    {.line-numbers}
    1
    2
    v += mu * v - learning_rate * dx
    x += v

其中一般的，v初始为0，mu是优化参数，一般初始化参数为0.9，当使用交叉验证的时候，参数mu一般设置成[0.5,0.9,0.95,0.99]，在开始训练的时候，梯度下降较快，可以设置mu为0.5，在一段时间后逐渐变慢了，mu可以设置为0.9、0.99。也正是因为有了“惯性”，这个比SGD会稳定一些。

4.CE交叉熵 与 BCE二分类交叉熵

二者是不一样的。参见(CE and BCE)[https://zhuanlan.zhihu.com/p/48078990]

5.BP算法

BP算法的整体思路如下：对于每个给定的训练样本，首先进行前向计算，计算出网络中每一层的激活值和网络的输出。对于最后一层(输出层)，我们可以直接计算出网络的输出值与已经给出的标签值(label)直接的差距，我们将这个值定义为残差δ。对于输出层之前的隐藏层L，我们将根据L+1层各节点的加权平均值来计算第L层的残差。
插入一些我个人对BP算法的一点比较容易理解的解释(如有错误请指出)：在反向传播 过程中，若第x层的a节点通过权值W对x+1层的b节点有贡献，则在反向传播过程中，梯度通过权值W从b节点传播回a节点。不管下面的公式推导，还是后面的卷积神经网络，在反向传播的过程中，都是遵循这样的一个规律。

6.anchor的还原。

Q:在SSD YOLO 以及Faster-RCNN中均提出了一个anchor的概念,所以问题产生了:在feature map上产生的anchor是在怎么还原到原图上的呢?

  • Faster R-CNN
    Faster RCNN中采用33卷积 padding为1，然后经过2\2的pooling。输出的尺寸刚好类似于将原始图片进行了resize。故将anchor直接还原。(等待少卿确认)
  • SSD 中采用了类似的结构??

7.关于卷积的一些看法

顺便吐槽一下CNN结构:我们在做网络结构分析或网络结构设计的时候，经常会有这样的感觉，输出的数想让它代表什么就代表什么，有时候甚至看起来很没有道理，但是最后这样的操作却能有效果，最重要的原因就在于卷积操作是没有实际的意义的，它只是很强的抽取能力，但是它并不知道会抽取出什么东西，所以如果我们设计合适的损失函数，就可以任意指定输出，哪怕这种指定看起来并没有道理。CNN本质上就是连接input与output之间的一个极其复杂的，表达能力很强的，并且很有潜力的函数，但是这个函数最终的能力能不能充分发挥出来，要取决于很多东西，损失函数，训练技巧，数据集等等。
ref

8.转置卷积。


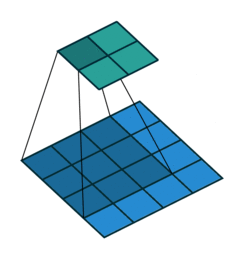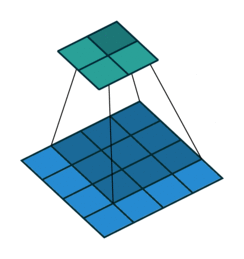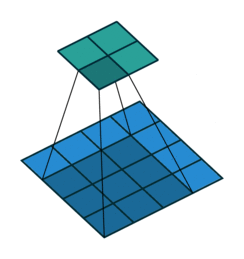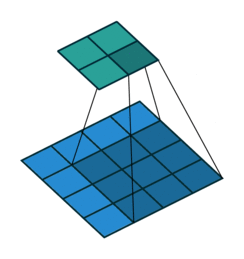
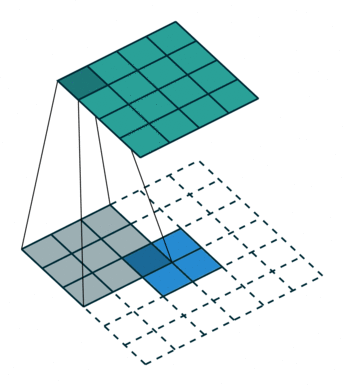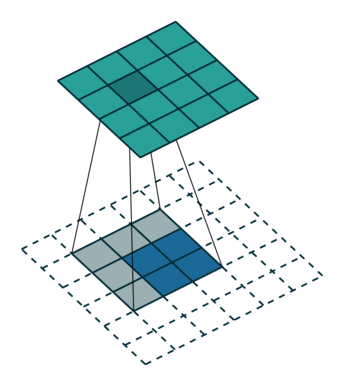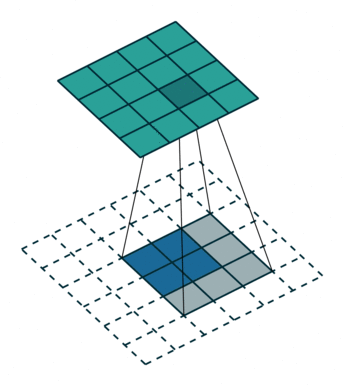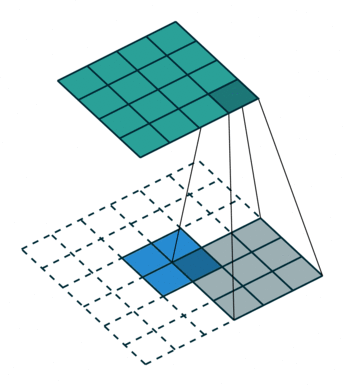
注意图中蓝色（下面）是输入，绿色（上面）是输出，卷积和反卷积在 p、s、k p、s、k 等参数一样时，是相当于 i i 和 o o 调了个位。
这里说明了反卷积的时候，是有补0的，即使人家管这叫no padding（ p=0 p=0），这是因为卷积的时候从蓝色 4×4 4×4 缩小为绿色 2×2 2×2，所以对应的 p=0 p=0 反卷积应该从蓝色 2×2 2×2 扩展成绿色 4×4 4×4。而且转置并不是指这个 3×3 3×3 的核 w变为 w.T，但如果将卷积计算写成矩阵乘法（在程序中，为了提高卷积操作的效率，就可以这么干，比如tensorflow中就是这种实现）， Y-> =CX-> （其中 Y->表示将Y→ 拉成一维向量， XX→ 同理），那么反卷积确实可以表示为 C.TY→，而这样的矩阵乘法，恰恰等于 W左右翻转再上下翻转后与补0的 Y 卷积的情况。

然后就产生了第三个confuse：“补0了会不会有影响，还能通过反卷积近似输入 X吗？”其实反卷积也不一定能达到近似的效果，图像里的卷积，相当于一种相关操作，而反卷积维持了这种相关操作时的 w与 X、与 Y 之间的联系维持了。至于补0后操作是否还等价，上一段已经说明了是等价的，读者可以在阅读完后面的文章后自己尝试一下。
tensorflow也是这样实现反卷积的。

9.对NN的核心贡献

  • 目前来看，很多对 NN 的贡献（特别是核心的贡献），都在于NN的梯度流上，比如：
    • sigmoid会饱和，造成梯度消失，于是有了ReLU。
    • ReLU负半轴是死区，造成梯度变0，于是有了LeakyReLU，PReLU。
    • 强调梯度和权值分布的稳定性，由此有了ELU，以及较新的SELU。
    • 太深了，梯度传不下去，于是有了highway。
    • 干脆连highway的参数都不要，直接变残差，于是有了ResNet。
    • 强行稳定参数的均值和方差，于是有了BatchNorm。
    • 在梯度流中增加噪声，于是有了 Dropout。
    • RNN梯度不稳定，于是加几个通路和门控，于是有了LSTM。
    • LSTM简化一下，有了GRU。
    • GAN的JS散度有问题，会导致梯度消失或无效，于是有了WGAN。
    • WGAN对梯度的clip有问题，于是有了WGAN-GP。

10.超清楚的优化算法讲解。看完豁然开朗。

简书
segment

发表于 | 分类于
Symbols count in article： 1.7k | Reading time ≈ 3 mins.

TCP/UDP 共用端口问题。

1.TCP UDP 可以共同占用一个端口号吗?

首先明确一点 端口是一种抽象的软件结构（包括一些数据结构和I/O缓冲区）。
应用程序（即进程）通过系统调用与某端口建立连接（binding）后，传输层传给该端口的数据都被相应进程所接收，相应进程发给传输层的数据都通过该端口输出。在TCP/IP协议的实现中，端口操作类似于一般的I/O操作，进程获取一个端口，相当于获取本地唯一的I/O文件，可以用一般的读写原语访问之。
类似于文件描述符，每个端口都拥有一个叫端口号（port number）的整数型标识符，用于区别不同端口。由于TCP/IP传输层的两个协议TCP和UDP是完全独立的两个软件模块，因此各自的端口号也相互独立，如TCP有一个255号端口，UDP也可以有一个255号端口，二者并不冲突。

2.为什么一个80端口可以建立很多连接?

一个TCP连接需要由四元组来形成，即(src_ip,src_port,dst_ip,dst_port)。假设有客户端建立了连接(src_ip1,src_port1,dst_ip1,dst_port1)，那么，如果我们还有listen在(src_ip1,src_port1)，那么当(dst_ip1,dst_port1)发送消息过来，系统应该把消息给谁？所以就说明了客户端占用了某一端口时，该端口就不能被其它进程listen了。

那么，对于有些童鞋，可能还有这样的疑问，是否一台机器就只能建立65535个连接了（端口16位限制）？非也，一个连接由四元组(src_ip,src_port,dst_ip,dst_port)形式，那么当(src_ip,src_port)一定时，变化的(dst_ip,dst_port)就可以建立更多连接了。
所以一台机器可以建立最多65535个连接是大错特错的。所有的一切都可以用四元组原理来分析即：一个TCP连接需要由四元组来形成，即(src_ip,src_port,dst_ip,dst_port),只要四个元素的组合中有一个元素不一样，那就可以区别不同的连接。

3.承接2问 为什么还会出现端口被占的情况？？

这个问题问的好。默认情况下 一个网络应用程序的套接字绑定了一个端口 这时候别的套接字就无法使用这个端口。这个就是为什么我们实际应用过程中经常会出现 端口已经被使用的情况。

但是 在实际网络编程过程中，socket有一个 SO_REUSEADDR 选项。该选项可以用在以下四种情况下。 (摘自《Unix网络编程》卷一，即UNPv1)

1、当有一个有相同本地地址和端口的socket1处于TIME_WAIT状态时，而你启动的程序的socket2要占用该地址和端口，你的程序就要用到该选项。
2、SO_REUSEADDR允许同一port上启动同一服务器的多个实例(多个进程)。但每个实例绑定的IP地址是不能相同的。在有多块网卡或用IP Alias技术的机器可以测试这种情况。
3、SO_REUSEADDR允许单个进程绑定相同的端口到多个socket上，但每个socket绑定的ip地址不同。这和2很相似，区别请看UNPv1。
4、SO_REUSEADDR允许完全相同的地址和端口的重复绑定。但这只用于UDP的多播，不用于TCP。

4.ftp端口的占用。

FTP服务器有两个端口，其中21端口用于连接，20端口用于传输数据.
进行FTP文件传输中，客户端首先连接到FTP服务器的21端口，进行用户的认证，认证成功后，要传输文件时，服务器会开一个端口为20来进行传输数据文件。
也就是说，端口20才是真正传输所用到的端口，端口21只用于FTP的登陆认证。我们平常下载文件时，会遇到下载到99%时，文件不完成，不能成功的下载。其实是因为文件下载完毕后，还要在21端口再行进行用户认证，而下载文件的时间如果过长，客户机与服务器的21端口的连接会被服务器认为是超时连接而中断掉，就是这个原因。解决方法就是设置21端口的响应时间。

发表于 | 分类于
Symbols count in article： 980 | Reading time ≈ 2 mins.

1.全排列

  • 1 字典序法………………………………………………………………………..

    字典序法主要用来求下一个方便。如果要完全遍历 字典序法并不是比较好的选择。时间还是比较复杂的,需要比较n!次
    字典序法的主要步骤为：

      1. 对于序列A 从右至左 找出第一个左边小于右边的数字。并记下其位置i.
      1. 继续对该序列 从右至左 找出第一个比A[i] 大的数字 记下其位置j(要保证j>i). 由于A[i]右侧的数字是递增的。在A[i]的右边的数字中，找出所有比A[i]大的数中最小的数字A[j]，即 j=max{i|pj>pi}（右边的数从右至左是递增的，因此j是所有大于A[i]的数字中序号最大者）
      1. 交换 A序列 i j 位置的值即A[i] 和 A[j]的值.
      1. 反转序列 A[i+1]A[i+2]…A[j]
      1. 反转之后的序列即为当前排列的下一排列。
        那么是如何得到的呢，我们通过观察原数组可以发现，如果从末尾往前看，数字逐渐变大，到了2时才减小的，然后我们再从后往前找第一个比2大的数字，是3，那么我们交换2和3，再把此时3后面的所有数字转置一下即可，步骤如下：

1　　2　　7　　4　　3　　1

1　　2　　7　　4　　3　　1

1　　3　　7　　4　　2　　1

1　　3　　1　　2　　4　　7

    1. 递归求解。主要思想是动态规划：即当前任务的完成是在上一个任务的基础上的。对已N个数 每个数轮流做开头 我们只需对剩余N-1个数的全排列即可，把第N个数放在N-1个数的全排列的开头就构成了N个数的全排列。这个明显的缺点就是有重复问题。
      1. 解决重复问题的方法：避免重复的数字做开头就好啦。递归操作时也是如此。保证的重复元素避免多次排列。

2.组合.

对于数组[1,2,3,4,5,6],求任意3个数的组合。

    1. 同样可以使用递归的思路。对于没有重复元素的数组 对于第一个数选择要或者不要。如果要就从剩余的数中选择出2个数(递归问题)。如果不要 就从剩余的数中选出3个数(递归问题)。
    1. 关于去重：去重的话只要判断在第i个位置是否已经出现过某数字 有的话 跳过.比如对 1 2 2 选两个数字进行排列.已经有了 [1 2] 时 第二个 [1] + [2]就直接跳过。

    相关问题汇总于C++版排列组合问题全解

发表于 | 分类于
Symbols count in article： 111 | Reading time ≈ 1 mins.

1.2018-11-14

内推了百度 CV相关岗位。打电话电话面 刚好要出门出差 我拒绝。然后他又说有时间了去公司面 当时项目比较赶 我拒绝。我并建议”有时间晚上再打电话过来吧” 电话那头 冷笑一声 “好的 谢谢”。
遂卒。

发表于 | 分类于
Symbols count in article： 153 | Reading time ≈ 1 mins.

1.保存修改的容器至镜像。

1
2
docker commit {id 前3位即可} your/name
docker save -o 要保存的文件名  要保存的镜像

2.加载镜像命令

1
docker load < filename

3.加载镜像之后 便可以通过加载的镜像创建容器并进入容器

发表于 | 分类于
Symbols count in article： 431 | Reading time ≈ 1 mins.

1.如何参与开源项目

  • 1.开通自己github账户，在PC端安装git环境。
  • 2.fork开源项目到仓库。
  • 3.clone远程forked项目到本地。
  • 4.添加上游

  • 5.同步远程原始项目到本地

    1
    git fetch upstream

  • 6.合并项目。

    1
    git merge upstream/master

  • 7.接下来正常add commit即可。

2.不小心添加了过大文件

如果不小心添加了过大文件到暂存区，无论是删除本地文件还是修改.gitingnore文件都是比较棘手的。
比较简单的做法是：

    1. git log查看commit日志
    1. git reset XXX 重装到某一提交状态。其中XXX为你某次提交的唯一ID如
      commit aa534e5ae59ac5b0df1e20dde8409c2f5d32b015，可以通过git log看到。只需输入前四位即可完成reset。
      然后只需正常输出 git add commit push等命令。